1. The Statcast revolution¶

This is Aaron Judge. Judge is one of the physically largest players in Major League Baseball standing 6 feet 7 inches (2.01 m) tall and weighing 282 pounds (128 kg). He also hit the hardest home run ever recorded. How do we know this? Statcast.
Statcast is a state-of-the-art tracking system that uses high-resolution cameras and radar equipment to measure the precise location and movement of baseballs and baseball players. Introduced in 2015 to all 30 major league ballparks, Statcast data is revolutionizing the game. Teams are engaging in an "arms race" of data analysis, hiring analysts left and right in an attempt to gain an edge over their competition. This video describing the system is incredible.
In this notebook, we're going to wrangle, analyze, and visualize Statcast data to compare Mr. Judge and another (extremely large) teammate of his. Let's start by loading the data into our Notebook. There are two CSV files, judge.csv and stanton.csv, both of which contain Statcast data for 2015-2017. We'll use pandas DataFrames to store this data. Let's also load our data visualization libraries, matplotlib and seaborn.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# Load Aaron Judge's Statcast data
judge = pd.read_csv('datasets/judge.csv')
# Load Giancarlo Stanton's Statcast data
stanton = pd.read_csv('datasets/stanton.csv')
%%nose
import pandas as pd
def test_judge_correctly_loaded():
correct_judge = pd.read_csv("datasets/judge.csv")
assert correct_judge.equals(judge), "The variable judge should contain the data in judge.csv."
def test_stanton_correctly_loaded():
correct_stanton = pd.read_csv("datasets/stanton.csv")
assert correct_stanton.equals(stanton), "The variable stanton should contain the data in stanton.csv."
2. What can Statcast measure?¶
The better question might be, what can't Statcast measure?
Starting with the pitcher, Statcast can measure simple data points such as velocity. At the same time, Statcast digs a whole lot deeper, also measuring the release point and spin rate of every pitch.
Moving on to hitters, Statcast is capable of measuring the exit velocity, launch angle and vector of the ball as it comes off the bat. From there, Statcast can also track the hang time and projected distance that a ball travels.
Let's inspect the last five rows of the judge DataFrame. You'll see that each row represents one pitch thrown to a batter. You'll also see that some columns have esoteric names. If these don't make sense now, don't worry. The relevant ones will be explained as necessary.
# Display all columns (pandas will collapse some columns if we don't set this option)
pd.set_option('display.max_columns', None)
# Display the last five rows of the Aaron Judge file
judge.tail()
%%nose
last_output = _
def test_head_output():
try:
assert "3431 CH" in last_output.to_string()
except AttributeError:
assert False, "Please use judge.tail() as the last line of code in the cell to inspect the data, not the display() or print() functions."
except AssertionError:
assert False, "The output of the cell is not what we expected. You should see 'CH' for pitch_type with index 3431 in the first of the five rows displayed using the tail() method."
3. Aaron Judge and Giancarlo Stanton, prolific sluggers¶

This is Giancarlo Stanton. He is also a very large human being, standing 6 feet 6 inches tall and weighing 245 pounds. Despite not wearing the same jersey as Judge in the pictures provided, in 2018 they will be teammates on the New York Yankees. They are similar in a lot of ways, one being that they hit a lot of home runs. Stanton and Judge led baseball in home runs in 2017, with 59 and 52, respectively. These are exceptional totals - the player in third "only" had 45 home runs.
Stanton and Judge are also different in many ways. One is batted ball events, which is any batted ball that produces a result. This includes outs, hits, and errors. Next, you'll find the counts of batted ball events for each player in 2017. The frequencies of other events are quite different.
# All of Aaron Judge's batted ball events in 2017
judge_events_2017 = judge.loc[judge['game_year'] == 2017].events
print("Aaron Judge batted ball event totals, 2017:")
print(judge_events_2017.value_counts())
# All of Giancarlo Stanton's batted ball events in 2017
stanton_events_2017 = stanton.loc[stanton['game_year'] == 2017].events
print("\nGiancarlo Stanton batted ball event totals, 2017:")
print(stanton_events_2017.value_counts())
%%nose
def test_judge_events_2017_correct():
correct_judge_events_2017 = judge.loc[judge['game_year'] == 2017].events
assert correct_judge_events_2017.equals(judge_events_2017), "The variable judge_events_2017 should contain the events column from the judge DataFrame after filtering for all pitches that occurred in 2017."
def test_stanton_events_2017_correct():
correct_stanton_events_2017 = stanton.loc[stanton['game_year'] == 2017].events
assert correct_stanton_events_2017.equals(stanton_events_2017), "The variable stanton_events_2017 should contain the events column from the stanton DataFrame after filtering for all pitches that occurred in 2017."
4. Analyzing home runs with Statcast data¶
So Judge walks and strikes out more than Stanton. Stanton flies out more than Judge. But let's get into their hitting profiles in more detail. Two of the most groundbreaking Statcast metrics are launch angle and exit velocity:
- Launch angle: the vertical angle at which the ball leaves a player's bat
- Exit velocity: the speed of the baseball as it comes off the bat
This new data has changed the way teams value both hitters and pitchers. Why? As per the Washington Post:
Balls hit with a high launch angle are more likely to result in a hit. Hit fast enough and at the right angle, they become home runs.
Let's look at exit velocity vs. launch angle and let's focus on home runs only (2015-2017). The first two plots show data points. The second two show smoothed contours to represent density.
# Filter to include home runs only
judge_hr = judge.loc[judge['events'] == 'home_run']
stanton_hr = stanton.loc[stanton['events'] == 'home_run']
# Create a figure with two scatter plots of launch speed vs. launch angle, one for each player's home runs
fig1, axs1 = plt.subplots(ncols=2, sharex=True, sharey=True)
sns.regplot(x='launch_angle', y='launch_speed', fit_reg=False, color='tab:blue', data=judge_hr, ax=axs1[0]).set_title('Aaron Judge\nHome Runs, 2015-2017')
sns.regplot(x='launch_angle', y='launch_speed', fit_reg=False, color='tab:blue', data=stanton_hr, ax=axs1[1]).set_title('Giancarlo Stanton\nHome Runs, 2015-2017')
# Create a figure with two KDE plots of launch speed vs. launch angle, one for each player's home runs
fig2, axs2 = plt.subplots(ncols=2, sharex=True, sharey=True)
sns.kdeplot(judge_hr.launch_angle, judge_hr.launch_speed, cmap="Blues", shade=True, shade_lowest=False, ax=axs2[0]).set_title('Aaron Judge\nHome Runs, 2015-2017')
sns.kdeplot(stanton_hr.launch_angle, stanton_hr.launch_speed, cmap="Blues", shade=True, shade_lowest=False, ax=axs2[1]).set_title('Giancarlo Stanton\nHome Runs, 2015-2017')
%%nose
import pandas as pd
def test_judge_hr_correct():
correct_judge_hr = judge.loc[judge['events'] == 'home_run']
assert correct_judge_hr.equals(judge_hr), "The variable judge_hr should contain all pitches in judge that resulted in a home run."
def test_stanton_hr_correct():
correct_stanton_hr = stanton.loc[stanton['events'] == 'home_run']
assert correct_stanton_hr.equals(stanton_hr), "The variable stanton_hr should contain all pitches in stanton that resulted in a home run."
# No standard testing procedure exists for plots at the moment
5. Home runs by pitch velocity¶
It appears that Stanton hits his home runs slightly lower and slightly harder than Judge, though this needs to be taken with a grain of salt given the small sample size of home runs.
Not only does Statcast measure the velocity of the ball coming off of the bat, it measures the velocity of the ball coming out of the pitcher's hand and begins its journey towards the plate. We can use this data to compare Stanton and Judge's home runs in terms of pitch velocity. Next you'll find box plots displaying the five-number summaries for each player: minimum, first quartile, median, third quartile, and maximum.
# Combine the Judge and Stanton home run DataFrames for easy boxplot plotting
judge_stanton_hr = pd.concat([judge_hr, stanton_hr])
# Create a boxplot that describes the pitch velocity of each player's home runs
sns.boxplot(x='player_name', y='release_speed', color='tab:blue', data=judge_stanton_hr).set_title('Home Runs, 2015-2017')
%%nose
def test_judge_stanton_hr_correct():
correct_judge_stanton_hr = pd.concat([judge_hr, stanton_hr])
also_correct_judge_stanton_hr = pd.concat([stanton_hr, judge_hr])
assert correct_judge_stanton_hr.equals(judge_stanton_hr) or \
also_correct_judge_stanton_hr.equals(judge_stanton_hr), \
"The variable judge_stanton_hr should be the concatenation of judge_hr and stanton_hr."
# No standard testing procedure exists for plots at the moment
6. Home runs by pitch location (I)¶
So Judge appears to hit his home runs off of faster pitches than Stanton. We might call Judge a fastball hitter. Stanton appears agnostic to pitch speed and likely pitch movement since slower pitches (e.g. curveballs, sliders, and changeups) tend to have more break. Statcast does track pitch movement and type but let's move on to something else: pitch location. Statcast tracks the zone the pitch is in when it crosses the plate. The zone numbering looks like this (from the catcher's point of view):
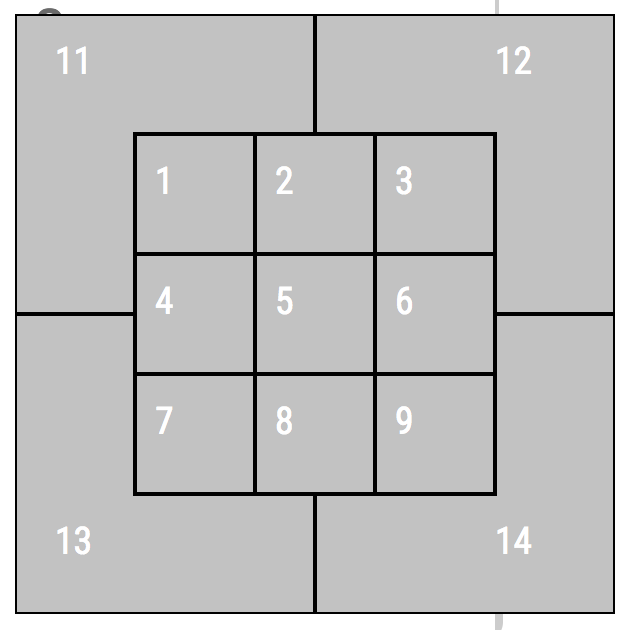
We can plot this using a 2D histogram. For simplicity, let's only look at strikes, which gives us a 9x9 grid. We can view each zone as coordinates on a 2D plot, the bottom left corner being (1,1) and the top right corner being (3,3). Let's set up a function to assign x-coordinates to each pitch.
def assign_x_coord(row):
"""
Assigns an x-coordinate to Statcast's strike zone numbers. Zones 11, 12, 13,
and 14 are ignored for plotting simplicity.
"""
# Left third of strike zone
if row.zone in [1, 4, 7]:
return 1
# Middle third of strike zone
if row.zone in [2, 5, 8]:
return 2
# Right third of strike zone
if row.zone in [3, 6, 9]:
return 3
%%nose
def test_assign_x_coord():
dummy_zone_x = [{'zone': 1},
{'zone': 2},
{'zone': 3},
{'zone': 4},
{'zone': 5},
{'zone': 6},
{'zone': 7},
{'zone': 8},
{'zone': 9}]
df_dummy_zone_x = pd.DataFrame(dummy_zone_x)
df_dummy_zone_x['zone_x'] = df_dummy_zone_x.apply(assign_x_coord, axis=1)
correct_zone_x = [{'zone': 1, 'zone_x': 1},
{'zone': 2, 'zone_x': 2},
{'zone': 3, 'zone_x': 3},
{'zone': 4, 'zone_x': 1},
{'zone': 5, 'zone_x': 2},
{'zone': 6, 'zone_x': 3},
{'zone': 7, 'zone_x': 1},
{'zone': 8, 'zone_x': 2},
{'zone': 9, 'zone_x': 3}]
df_correct_zone_x = pd.DataFrame(correct_zone_x)
assert df_correct_zone_x.equals(df_dummy_zone_x), "At least one of the zone's assigned x-coordinates are incorrect."
7. Home runs by pitch location (II)¶
And let's do the same but for y-coordinates.
def assign_y_coord(row):
"""
Assigns a y-coordinate to Statcast's strike zone numbers. Zones 11, 12, 13,
and 14 are ignored for plotting simplicity.
"""
# Upper third of strike zone
if row.zone in [1, 2, 3]:
return 3
# Middle third of strike zone
if row.zone in [4, 5, 6]:
return 2
# Lower third of strike zone
if row.zone in [7, 8, 9]:
return 1
%%nose
def test_assign_y_coord():
dummy_zone_y = [{'zone': 1},
{'zone': 2},
{'zone': 3},
{'zone': 4},
{'zone': 5},
{'zone': 6},
{'zone': 7},
{'zone': 8},
{'zone': 9}]
df_dummy_zone_y = pd.DataFrame(dummy_zone_y)
df_dummy_zone_y['zone_y'] = df_dummy_zone_y.apply(assign_y_coord, axis=1)
correct_zone_y = [{'zone': 1, 'zone_y': 3},
{'zone': 2, 'zone_y': 3},
{'zone': 3, 'zone_y': 3},
{'zone': 4, 'zone_y': 2},
{'zone': 5, 'zone_y': 2},
{'zone': 6, 'zone_y': 2},
{'zone': 7, 'zone_y': 1},
{'zone': 8, 'zone_y': 1},
{'zone': 9, 'zone_y': 1}]
df_correct_zone_y = pd.DataFrame(correct_zone_y)
assert df_correct_zone_y.equals(df_dummy_zone_y), "At least one of the zone's assigned y-coordinates are incorrect."
8. Aaron Judge's home run zone¶
Now we can apply the functions we've created then construct our 2D histograms. First, for Aaron Judge (again, for pitches in the strike zone that resulted in home runs).
# Zones 11, 12, 13, and 14 are to be ignored for plotting simplicity
judge_strike_hr = judge_hr.copy().loc[judge_hr.zone <= 9]
# Assign Cartesian coordinates to pitches in the strike zone for Judge home runs
judge_strike_hr['zone_x'] = judge_strike_hr.apply(assign_x_coord, axis=1)
judge_strike_hr['zone_y'] = judge_strike_hr.apply(assign_y_coord, axis=1)
# Plot Judge's home run zone as a 2D histogram with a colorbar
plt.hist2d(judge_strike_hr.zone_x, judge_strike_hr.zone_y, bins = 3, cmap='Blues')
plt.title('Aaron Judge Home Runs on\n Pitches in the Strike Zone, 2015-2017')
plt.gca().get_xaxis().set_visible(False)
plt.gca().get_yaxis().set_visible(False)
cb = plt.colorbar()
cb.set_label('Counts in Bin')
%%nose
def test_judge_strike_hr_correct():
correct_judge_strike_hr = judge_hr.copy().loc[judge_hr.zone <= 9]
correct_judge_strike_hr['zone_x'] = correct_judge_strike_hr.apply(assign_x_coord, axis=1)
correct_judge_strike_hr['zone_y'] = correct_judge_strike_hr.apply(assign_y_coord, axis=1)
assert correct_judge_strike_hr.equals(judge_strike_hr), "The zone_x and zone_y columns of judge_strike_hr should contain each zone's Cartesian coordinates."
# No standard testing procedure exists for plots at the moment
9. Giancarlo Stanton's home run zone¶
And now for Giancarlo Stanton.
# Zones 11, 12, 13, and 14 are to be ignored for plotting simplicity
stanton_strike_hr = stanton_hr.copy().loc[stanton_hr.zone <= 9]
# Assign Cartesian coordinates to pitches in the strike zone for Stanton home runs
stanton_strike_hr['zone_x'] = stanton_strike_hr.apply(assign_x_coord, axis=1)
stanton_strike_hr['zone_y'] = stanton_strike_hr.apply(assign_y_coord, axis=1)
# Plot Stanton's home run zone as a 2D histogram with a colorbar
plt.hist2d(stanton_strike_hr.zone_x, stanton_strike_hr.zone_y, bins = 3, cmap='Blues')
plt.title('Giancarlo Stanton Home Runs on\n Pitches in the Strike Zone, 2015-2017')
plt.gca().get_xaxis().set_visible(False)
plt.gca().get_yaxis().set_visible(False)
cb = plt.colorbar()
cb.set_label('Counts in Bin')
%%nose
def test_stanton_strike_hr_correct():
correct_stanton_strike_hr = stanton_hr.copy().loc[stanton_hr.zone <= 9]
correct_stanton_strike_hr['zone_x'] = correct_stanton_strike_hr.apply(assign_x_coord, axis=1)
correct_stanton_strike_hr['zone_y'] = correct_stanton_strike_hr.apply(assign_y_coord, axis=1)
assert correct_stanton_strike_hr.equals(stanton_strike_hr), "The zone_x and zone_y columns of stanton_strike_hr should contain each zone's Cartesian coordinates."
# No standard testing procedure exists for plots at the moment
10. Should opposing pitchers be scared?¶
A few takeaways:
- Stanton does not hit many home runs on pitches in the upper third of the strike zone.
- Like pretty much every hitter ever, both players love pitches in the horizontal and vertical middle of the plate.
- Judge's least favorite home run pitch appears to be high-away while Stanton's appears to be low-away.
- If we were to describe Stanton's home run zone, it'd be middle-inside. Judge's home run zone is much more spread out.
The grand takeaway from this whole exercise: Aaron Judge and Giancarlo Stanton are not identical despite their superficial similarities. In terms of home runs, their launch profiles, as well as their pitch speed and location preferences, are different.
Should opposing pitchers still be scared?
# Should opposing pitchers be wary of Aaron Judge and Giancarlo Stanton
should_pitchers_be_scared = True
%%nose
def test_scared():
assert should_pitchers_be_scared == True, "Pitchers should be scared of Aaron Judge and Giancarlo Stanton! They are scary!"